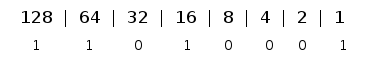Binary, Hexadecimal, and Decimal
In most math we do from day to day we use the numbers 0-9, which is a base 10 numbering system since it uses 10 digits. Base 10 is known as decimal. Binary is a base 2 numbering system. It uses only 0 and 1 as digits. Hexadecimal is a bit more complicated, its a base 16 numbering system. Hexadecimal uses 0-9 just like decimal, but it also uses A-F to represent 10-15 respectively.
In order to pass your CCNA exam you will need to know how to convert between base 2, base 10, and base 16. I'll go over the process of converting each to each other.
In order to pass your CCNA exam you will need to know how to convert between base 2, base 10, and base 16. I'll go over the process of converting each to each other.
Decimal to Binary Conversion
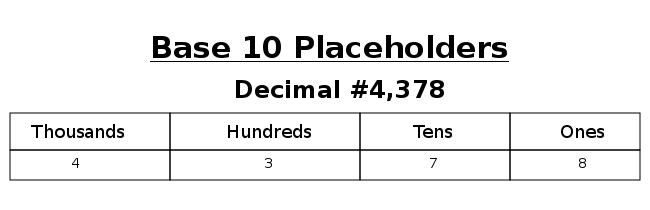
There are many different ways to do decimal and binary conversions. The method I'm going to show you is how I learned. Decimal numbers have place holders representing ones, tens, hundreds, thousands, etc.
Binary placeholders are similar but are ordered in factor of 2's. Take a look at the following image -
As you can see the binary place holders begin with 0 and progress through the factors of 2. If we were to convert a number into binary we would start by finding the largest placeholder that is not above the number we are converting and subtracting it from the decimal number. We would repeat this process until the decimal number is subtracted to 0. The following image displays the process of converting the decimal number 82 to binary.
As you can see from the above image the decimal #82 = 01010010 in binary. Everywhere there is a 1 is considered 'on' and that placeholder should be counted. If we added up all of the bits that were on we would get 82. Using this process we can do the reverse conversion of binary to decimal.
Lets take the binary number 11010001 and convert it to decimal. The first thing we do is figure out which placeholders are turned on. So lets line the binary number up with our placeholders, and remember to always start at the 1 placeholder.
Lets take the binary number 11010001 and convert it to decimal. The first thing we do is figure out which placeholders are turned on. So lets line the binary number up with our placeholders, and remember to always start at the 1 placeholder.
All we have to do is add the placeholders up now. 128 + 64 + 16 + 1 = 209