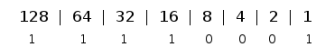Binary to Hexadecimal Conversion
Now that we know how to convert binary to decimal, lets take a look at how to convert binary to hexadecimal. Just like with decimal and binary we will be using placeholders to determine the hex number but the process is a little different for hex. Lets take the binary number 11101011 and convert it into hexadecimal.
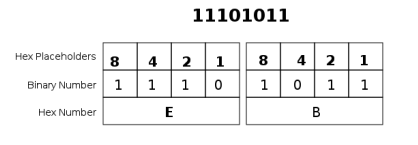
Each hexadecimal digit is actually 4 bits long, so the first step to the conversion process is to break down the binary number into groups of 4 bits. This gives us 2 groups 1110 and 1011. Each group of 4 bits is called a nibble. Take a look at the following image -
Each hexadecimal digit is actually 4 bits long, so the first step to the conversion process is to break down the binary number into groups of 4 bits. This gives us 2 groups 1110 and 1011. Each group of 4 bits is called a nibble. Take a look at the following image -
Notice that the hex placeholders are the same as the first 4 in binary. Since each digit is 4 bits this makes sense. All we do is add each placeholder that's turned on in each nibble. The first nibble has the 8, 4, and 2 placeholder turned on, so 8 + 4 + 2 = 14 . So our first digit is 14 and we see that the hex digit E represents 14 in the image. This is because after 0-9 hex begins using numbers to represent numbers with more than 1 digit, for example A=10 , B=11, C=12, D=13, E=14, F=16. So we see that 14 is represented by E in hex. The next nibble has the 8, 2, and 1 placeholders turned on. 8 + 2 + 1 = 11, and in hex 11 is represented by B. So our hex number is 0xEB (the 0x in the beginning of the number is used to represented hexadecimal numbers so that they are not confused with other numbering systems or words).
Now that we know how to convert decimal numbers to binary and binary numbers to hex we can convert decimal numbers to hex and back. Lets take the decimal number 109. Lets convert this into binary, and then into hex.
Now that we know how to convert decimal numbers to binary and binary numbers to hex we can convert decimal numbers to hex and back. Lets take the decimal number 109. Lets convert this into binary, and then into hex.
Lets start subtracting placeholders to find our binary number. The first placeholder we can subtract from 109 is 64. So we subtract that placeholder, 109 - 64 = 45. The next placeholder we can subtract is 32, so 45 - 32 = 13. The next placeholder is 8, 13 - 8 = 5, and then 5 - 4 = 1 and the last placeholder is 1, so 1 - 1 = 0. Perfect, so the 64, 32, 8, 4, and 1 placeholders are turned on in this decimal number giving us 01101101.
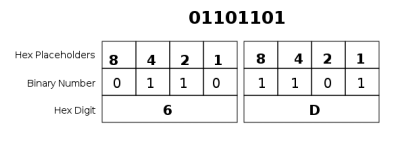
Now we convert this binary number into hex. First we break the binary number into nibbles giving us 0110 and 1101.
Now we convert this binary number into hex. First we break the binary number into nibbles giving us 0110 and 1101.
As we can see from the above image the first nibble has the 4, and 2 placeholders turned on giving it a value of 6, and the second nibble has the 8, 4, and 1 placeholders turned on giving it a value of 14, or D. This gives us a hex number of 0x6D. Now we know that 109 = 0x6D in hex. The same process is done except in reverse to convert a hex number to decimal.
Lets go ahead and do one more example, this time converting the opposite way. Lets take the hex number 0xF1. First step is to convert the hex into decimal. We know that F represents 15 in hex so we start subtracting placeholders. We subtract the first placeholder , 8 , since it's less than 15, which is 15 - 8 = 7. We then subtract the next placeholder 4 and get 7 - 4 = 3. Then subtract 2 to get 3 - 2 = 1, and subtract the last placeholder giving us 1 - 1 = 0. So our first nibble is 1111 in binary.
Lets do the same for our second nibble which is 1, this ones simple since the only thing we can subtract is the 1 placeholder giving us 0001 in this nibble. So our whole binary number will be 11110001. Now all we have to do is convert the binary number into decimal.
Lets go ahead and do one more example, this time converting the opposite way. Lets take the hex number 0xF1. First step is to convert the hex into decimal. We know that F represents 15 in hex so we start subtracting placeholders. We subtract the first placeholder , 8 , since it's less than 15, which is 15 - 8 = 7. We then subtract the next placeholder 4 and get 7 - 4 = 3. Then subtract 2 to get 3 - 2 = 1, and subtract the last placeholder giving us 1 - 1 = 0. So our first nibble is 1111 in binary.
Lets do the same for our second nibble which is 1, this ones simple since the only thing we can subtract is the 1 placeholder giving us 0001 in this nibble. So our whole binary number will be 11110001. Now all we have to do is convert the binary number into decimal.
The above image shows that the 128, 64, 32, 16, and 1 placeholders are turned on. Lets add them up to get our decimal number. 128 + 64 + 32 + 16 + 1 = 241. This means that our hex number 0xF1 = 241 in decimal.